建模研究/排队论模型和灵敏度检验分析( 二 ) _排队论

灵敏度分析用途：
主要用于模型检验和推广。简单来说就是改变模型原有的假设条件之后灵敏度计算，所得到的结果会发生多大的变化。
灵敏度分析举例：
数据是由测量，观察有时甚至完全猜测得到的，因此，我们要考虑数据不准确的可能性。
案例分析：

猪的重量w（磅），从现在到出售猪期间经历的时间t（天），t天内饲养猪的花费C（美元），猪的市场价格p（美元/磅），出售生猪所获得的收益R（美元），我们最终要获得的净收益P（美元）。还有一些其他量，如猪的初始重量200磅。
（建议先写显而易见的部分）
猪从200磅按每天5磅增加
（w磅）=（200磅）+（5磅/天）*（t天）
饲养每天花费45美分
（C美元）=（0.45美元/天）*（t天）
价格65美分按每天1美分下降
（p美元/磅）=（0.65美元/磅）-（0.01美元/磅）*（t天）
生猪收益
（R美元）=（p美元/磅）*（w磅）
净利润
（P美元）=（R美元）-（C美元）
用数学语言总结和表达如下：
参数设定：
t=时间（天）
w=猪的重量（磅）
p=猪的价格（美元/磅）
C=饲养t天的花费（美元）

R=出售猪的收益（美元）
P=净收益（美元）
假设：
w=200+5t
C=0.45t
p=0.65-0.01t
R=p*w
P=R-C
t>=0
目标：求P的最大值
第二步：选择建模方法
本例采用单变量最优化问题或极大—极小化问题
第三步：推导模型的数学表达式子
P=R-C（1）
R=p*w（2）
C=0.45t （3）
得到R=p*w-0.45t
p=0.65-0.01t （4）

w=200+5t（5）
得到P=（0.65-0.01t)(200+5t)-0.45t
令y=P是需最大化的目标变量，x=t是自变量，现在我们将问题转化为集合S={x:x>=0}上求函数的最大值：
y=f（x）=（0.65-0.01x)(200+5x)-0.45x
通过以上分析，得到，生猪现在的重量，现在的价格，每天饲养花费都很容易测量，而且有相当大的确定性。但是猪的生长率则不那么确定，而价格的下降率则确定性更低，记r为价格的下降率，现在假设r的实际值不同，对几个不同的r值重复前面的求解过程，我们会对问题的解关于r的敏感程度有所了解。下表给出了几个不同r值求出的计算结果。根据表格绘制图形，我们可以看到售猪的最优时间对参数r很敏感。

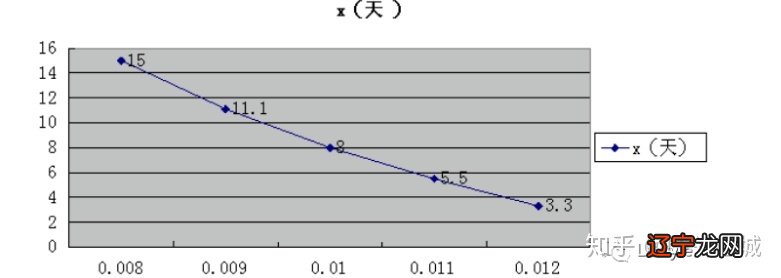
对灵敏度的更系统的分析是将r视为未知参数，按前面的步骤求解，写出p=0.65-rt 。得到y=f（x）=（0.65-rx）（200+5x）-0.45x 。使得导数为0，得到x=（7-500r）/25r，当x>=0时，只要0
对于猪的生长率g同样不确定，我们有w=200+gt，得到y=f（x）=（0.65-rx）（200+gx）-0.45x 。使得导数为0，得到x=5*(13g-49)/2g 。当x>=0时，得到g>=3.769 。
我们将灵敏度数据用相对改变量表示，例如：r下降10%导致了x增加了39%，而g下降了10%导致了x下降了34% 。
如果x的改变量Δx，则Δx/x表示相对改变量。如果r改变了Δr，导致了x有Δx的改变量，则相对改变量的比值为（Δx/x）/（Δr/r），令Δr→0，我们有（Δx/x）/（Δr/r）→（dx/dr）*（r/x）。我们称这个极限值为x对r的灵敏度，即为S（x，r）。

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：