一十二星座行业平均得分vs.行业得分表( 八 ) _星座

顺便提一下，人类在南北半球存在对称的差异性不是新的发现。有研究表明在北半球，出生在10，11，12月的人们的寿命比出生在4，5，6月的要长。而在南半球，结论正好相反（或相差6个月）（见【附三1】）。又有研究表明在北半球，出生在7，8，9月的妇女的生育率要比在其它月份出生的妇女低。而在南半球，结论正好相反（见【附三2】）。
【附三1】 and ,on Month of Birth, PNAS, Vol. 98, No. 5,27, 2001.
【附三2】Huber, , and , Month of Birth andCount of Women: Data from the, Human . 2008 May, 23(5)
附录四：人数分布方法检验
首先，简单回顾一下，本文主要讨论的是十二星座与天赋之间的关系。使用的方法是考察每一个行业中的星座人数分布。这里的星座人数分布是指十二星座中每个星座会被分配到一定的人数。
在本附录中，我就要来检验人数分布方法：如果我不按十二星座分配人数（星座人数分布），而是按十二月份分配人数（月份人数分布），情况是否会发生变化？我判断分布方法优劣的标准是看哪个方法更能反映人数的差异性，这里我用离散系数（ of，CV，定义为标准差与平均值之比）来衡量。举个极端的例子，假设按十二个月份分配人数，我得到了一个均匀分布（），那我就无从得知人数差异的有效信息（CV=0）观察星座有哪些现象，从而无法把它和天赋建立起关系。换句话说，CV越大，越能够反映人数的差异性，这正是本文所需要的。
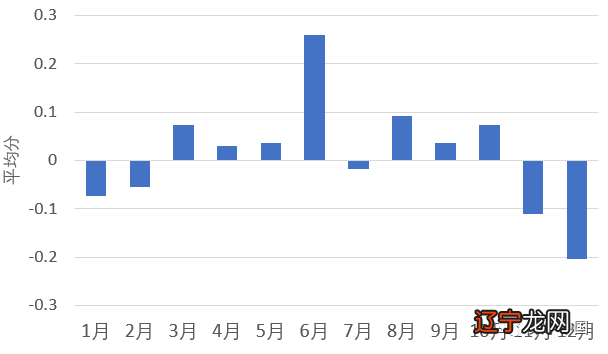
那么，真实情况如何呢？下表（附表一）总结了27个行业在两种人数分布中的离散系数，以及两者之差，和它们的统计显著性。如表所示，相较于月份人数分布CV，星座人数分布CV在27个行业中增大的多达16个，减少的只有8个。如果考虑二者之差的统计显著性（计算两个离散系数相同与否的假设检验方法，请见【附四1】），星座人数分布CV增大的行业个数也多于月份人数分布CV 。所以，从这个角度来说，使用星座人数分布方法要优于月份人数分布方法。另外，如果来观察十二月份的平均得分，我发现“波”消失了（见图B）。只有10月到3月，稍微有一点 “波” 的影子。我想一个很重要的原因就是因为月份与太阳的运行的关系不紧密。正因为此，我更感叹正文中图八的美妙！
附表一：人数分布对比

图B：十二月份行业平均得分（北半球）

【附四1】 of，（）
附录五：量子纠缠科普（学霸退散版）
什么是“量子纠缠”？通俗地讲就是相隔很远的两个物体可以瞬间影响彼此。这里说的“相隔很远”是多远呢？中国科学家最近（2017年6月）证实了至少在千公里级别的距离下，量子纠缠现象是存在的（见【附五1】）。我相信如果实验条件允许，更远距离的纠缠现象也能够被证实。

其次，什么叫“影响彼此”？这里就要引入“叠加态”的概念。著名的“杨氏双缝电子干涉实验”证明了电子可以同时穿过两条狭缝！这就是“叠加态”的体现：电子既在位置A，又在位置B 。更重要的是，当人们去观察电子如何同时穿过两条狭缝时，量子的模糊的叠加态“塌缩”了，变成了确定的状态，即人们只能看到电子出现在位置A，或在位置B 。所以，“互相影响彼此”的意思就是当其中一个物体状态发生改变（比如人们对其进行观测），另一个的状态会瞬时发生相应改变。这种“心灵感应”似的神秘关联被称为量子非定域性，爱因斯坦称其为“幽灵般的远距作用（at a ）” 。

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：

一 十二星座行业平均得分vs.行业得分表( 八 )

一十二星座行业平均得分vs.行业得分表( 八 )