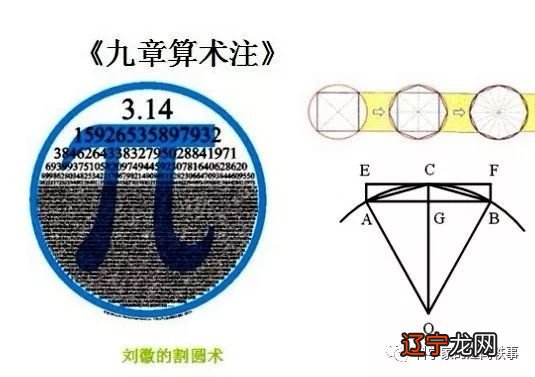
二【知识点】刘徽公式及计算圆周率的方法( 二 ) _数学

刘辉在用无限除法求解圆锥体积时提出的一个重要原则：将块（沿长方体的相对两条边切割平面得到的楔形固体）分解成阳马（右-角四棱锥）和龟臧（四边都是直角三角形的四面体），那么“羊马第二，龟第一，不容易”，即羊马的体积之比到乌龟的体积总是2：1 。这个原理是为了证明《九章算术》中提出的阳马体积公式
何龟体积公式
钥匙。上述原理和公式在长宽高不等的情况下是显而易见的，但刘辉认为，这不能简单地推广到长宽高不等的一般情况。于是他提出并用极限法证明了上述原理。

求解球体积的假设
《算术九章》中用球的体积来建立圆的公式等价于
，刘辉指出，这个公式是错误的，原因是球体与外接圆柱体的体积比被误认为是3：4 。刘辉设计了一个茅台方盖（两个相等圆柱体正交得到的公共部分，提出球体与茅台方盖的体积比为π:4，并指出解决问题的正确方法）球的体积公式。但他没能找到。但是刘辉是个谦虚的人，相信后天学习，意思是“会说话。”），得到了牟合方盖的体积，并得到了球体体积的正确公式。刘辉在证明先斜（楔形体）体积公式时，提出“上连无断，
费率的应用
刘辉给出的速率定义是：“任何匹配的数字都称为速率” 。他把分数看作两个量之和，指出率具有“厚者厚，薄者细”的性质，因此可以“相乘而散，近似为聚，统一连接” 。它是数学运算的大纲。他还提出“每九个数都可以作为章名，所有的比率都可以广泛应用”，《算术九章》提出了现在的技术——“所有数的乘法是真，数即法，真为真。法为一”是一般的方法。他用率，尤其是金有书，对《算术九章》中的大部分技术文章进行注释，近200题。他认为，只要我们能根据问题的数量关系（事物的形成率）找出每件事的发生率，并“平衡其偏差，平衡其不均匀性”，所有这些都可以归功于今天的技术。所谓“均衡偏差，对齐不均匀”，就是均衡的原理。刘辉不仅演示了分数运算、一般比、链比和比例分配问题（主要集中在方天、数米、下降、全损等章节），还演示了盈余技术和不足，
刘徽对数学做出了巨大贡献。他在天文观测中发展了重差技术，说：“有极高期望和绝对深度，知道距离的人，一定要用重差和毕达哥拉斯，而且一定要用重差作为比率，所以叫做重差。。” 他在《海岛算经》中提出了三种基本方法：重复法、连续索法、疲倦法，并得出“孤立者三观，超然者求其他的东西看起来四。”
刘辉提出了在无穷平方问题中求小数的思路。这种方法与后面求无理根逼近的方法是一致的。它不仅是精确计算圆周率的必要条件，而且促进了小数的产生。在线性方程组的求解中，他创造了一种互乘相消的方法，比直接除法更简单，与现在的解法基本相同。他还使用衰减技术来求解线性方程，创造了一种新的方程技术。他指出，“五企共享井”的解决方案是“按比例” 。他在中国数学史上第一次提出了不定方程问题。
刘辉认为，数学的范围是无穷无尽的，但研究起来并不难，因为它的方法都来自于客观世界中“规则”（空间形式）和“量度”（数量关系）的统一。刘徽通过“观阴阳之分，算术之根”，深刻领会了数学的精髓。他认为“物以类推，各有目的” 。因此中国传统术数学基础，数学就像一棵大树，虽然分出许多枝干，但根都相同。.

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：

二 【知识点】刘徽公式及计算圆周率的方法( 二 )

二【知识点】刘徽公式及计算圆周率的方法( 二 )