经济类 “高等数学”学生课程论文说明表（一）( 二 ) _数学

2.3 《易经》方法中的数论问题，其实是一个与数有关的活动，方法确实是一个计算活动。圣餐有很多种形式，现在让我们来分析一种圣餐。2.3.1《周一笑法》介绍将49株蓍草随机分成两堆，然后将其中一堆取出，剩余两堆蓍草分为one 把地分组，去掉小于4的余数（如果没有余数，则计算余数为余数4），所以把已经取出的那个相加，去掉根蓍草，剩下的4440根，这个过程叫做“一变同” 一个改变剩余的蓍草，重复上述过程，剩下的40、3<@6、或32个蓍草称为“两变” 。对剩余的蓍草重复上述过程，剩下的3<@6、32、28 24蓍草，称为“三改” 。四个数字之一。如果得到9或7，则称为阳耀，用“-”表示；如果得到 8 或 6，则称为印尧周易术数学原理，用“--”表示。就这样，“三变”决定了一个姚。这个过程重复六次，得到6个八卦，确定一个卦。六芒星的运算就完成了。《八卦》中的卦，预测占卜行为的好、坏、悔、悲等。每个卦有六个卦，卦是摇卦得来的周易术数学原理，规定卦只能摇一次。@二、第三次摇卦。顺序是从下到上。2.3.2《周一孝法》与一全等关系《周一》卦形法与一全等有关。同余论属于“数论”的范畴，是一种关于数可分性的符号语言。
【经济类 “高等数学”学生课程论文说明表（一）】

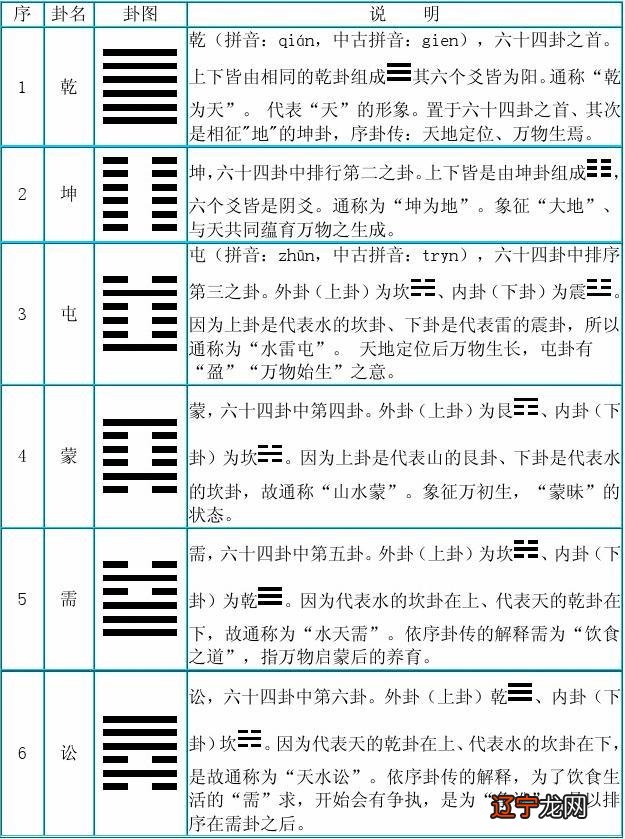
同余定理：（孙子定理）如果m是自然数，如果(ab)是m的倍数，则称为b(modm)，意思是：a-bmk(k是整数) 。64 《易经》中卦形成的巧妙方法是将49个蓍草用三种方式转化为21个，得到以下四种可能的数字之一：49=36, 48=32, 47=21, 46 =24 。这一定是《易经》作者通过精确的数学运算和反复试验得出的巧妙构思。这种巧思，从数学的角度来看，正是数论同余论的思想。周易中的分区就是不断重复以下两个操作：操作一：操作二：我们可以认为，《易经》中的卦象是同余公式的基础，而孙子定理发展了这一理论。2.4 《易经》中河图、洛书的数学奥秘有“天悬于天”、“河生图、洛生书、圣人法则”之说它” 。2.4.1 河图的由来关于“河出图”，据说伏羲一族征服了世界，黄河上的一头龙马载着一幅画作为礼物送给他。天地数之和为55 。东、西、南、北都是奇偶（阴阳）数相配，形成天地数。天地总数是55，也就是八卦中的大衍数。河图外数，阳线9、7；阴线 8 匹配阴阳线： 9+<@6、8+6 和为 15，而 15 是一个神秘的数字。2.4.2 相传，大禹治水的时候，一只乌龟从洛水里跳了出来，背着一张献给大禹的画。这幅画叫做《洛书》。九，大禹因之成就九域，世间大法。

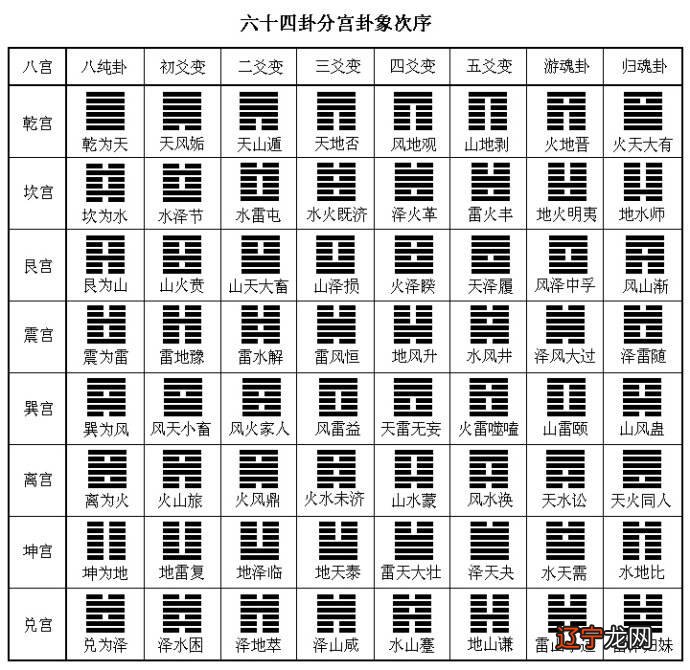
“河图”用青色书写，“洛书”用红色书写。白点代表阳：1、3、5、7、9 黑点代表阴：2、4、<@6、8 。洛书可译为数九宫格。后来研究了“河图”和“洛书” 。既然用十进制代替二进制计数是一个很大的变化，就必须普及和使用，于是便诞生了“和楚图图”、“洛楚书”等美丽的传说。九宫图又称纵横图，西方人称其为魔方。一开始纯粹是游戏，没有什么实用价值，历史上还夹杂着迷信。2.4.3 洛书和魔方魔方定义：一个由 n 个不同整数的平方组成的方阵，使得沿任何行、列以及主对角线和次对角线的 n 具有相同的和。统一的数称为“幻方常数” 。“洛书”翻译成今天的象征文字是“三阶魔方” 。这个小魔方蕴含着无穷无尽的数字和奥术：古今研究易经的人不计其数，很多人把河图和洛书当成魔方，因为河图和洛书既抽象又复杂。具体来说，数学的变化层出不穷，以至于很多人都着迷于探索其中的奥秘，以赶上时代的步伐。数学，作为自然科学的女王，是科学技术发展的基础，也是人类征服自然的有力武器。在《易经》丰富多彩的科学宝库中，数学是一颗闪耀千年的璀璨明珠。

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：