组图 5.桃李满天下为大师之师无缘( 二 ) _湍流

为流体力学倾注了数十年的心血和精力，湍流问题已成为他生活中的一个纠葛，经常困扰到他晚年。20世纪流体力学的权威、钱学森、郭永怀等人的老师冯卡门在自传中记录了这样一个事件：“德国著名理论物理学家索末菲曾告诉我，他生前希望能够理解两种现象——量子力学和湍流。”海森堡对这段话的说法略有不同：“索末菲说：当我看到上帝时，我想问他两个问题：为什么会有相对论？为什么会有湍流？”
无论是哪个版本，“动荡”这个词都包含在这个让索末菲终生困惑并试图向上帝寻求答案的问题中。难忘的梦，就是难忘！
·新的原子模型，解释谱线
除了考虑湍流之外，索末菲还有很深的数学基础，狭义相对论的数学基础，以及介质中的电磁波。也对传播做出了重要贡献
索末菲是本文主题的量子理论的创始人之一。他自己的贡献主要有：改进了玻尔原子模型，发现了精细结构常数。
玻尔1913年的原子模型很好地解释了氢原子谱线的分布，但仍然存在很多问题。首先，进一步的实验结果发现，氢原子的谱线结构精细，原来的谱线实际上是由几条谱线组成的；二是氢原子以外的许多电子的原子结构无法成功解释。

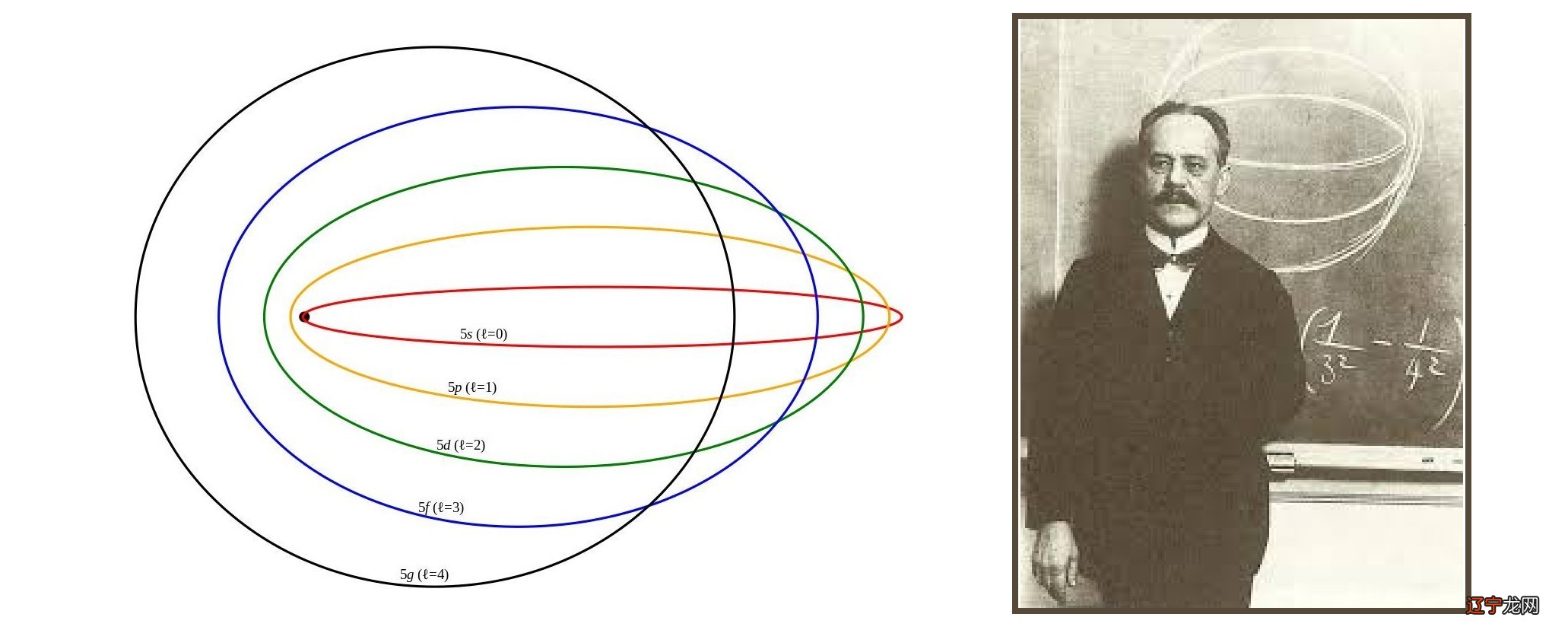
针对这些问题，索末菲在玻尔原子模型的基础上做了一些改进，建立了索末菲模型。索末菲的主要观点是，电子围绕原子核的轨道不一定是一个正圆，而是一个椭圆。玻尔模型中的圆形轨道对应于主量子数，而椭圆轨道的引入导致了几个额外的量子数。为此，索末菲首先提出了第二量子数（角量子数）和第四量子数（自旋量子数）的概念。

由于这些额外量子数的引入，电子轨道的能级不仅与主量子数n有关，还与角量子数l、自旋量子数s有关。此外，还有第三个量子数（磁量子数）m，它是角量子数l在Z轴上的投影。它的作用表现在原子受到外磁场作用时谱线的分裂，即正常的塞曼效应。其中，三个量子数n、l、m均取整数值，相互制约。角量子数不能超过主量子数，磁量子数不能超过角量子数。自旋量子数s只能取1/2和-1/2这两个值。
·精细结构常数意义重大
磁量子数可以解释正常的塞曼效应，自旋量子数可以解释反常的塞曼效应。从索末菲的原子模型中，我们知道不同角动量量子数的轨道之间的能级差与无量纲常数的平方成正比。索末菲在解释光谱的精细结构时引入了这个常数，现在称为“精细结构常数” 。
引入精细结构常数后，原子模型中电子的速度和能级可以用更紧凑的形式表示。后来，量子电动力学、统一理论等理论物理学的发展，赋予了精细结构常数更深的含义。将其精彩的内涵展现在世人面前。这是发现它的索末菲没有预料到的结果。简单地说，精细结构常数是电磁相互作用中电荷间耦合强度的量度，表征电磁相互作用的强度。该耦合常数的解释扩展到其他三个基本相互作用。换句话说，每个相互作用对应于一个耦合常数，其大小表征了相互作用的强度。例如：强相互作用的耦合常数约为1，约为电磁相互作用精细结构常数（1/137））的137倍，弱相互作用的耦合常数约为10- 13、与引力相互作用的耦合常数为10-39 。从这些数值中，我们可以大致知道四种交互强度的比较。
精细结构常数a是一种很奇怪的关系，电荷e、普朗克常数h和光速c联系在一起：

最后三个常数表征了现代物理学中的三种不同理论：电动力学、量子力学和相对论。它们 (e, h, c) 共同构成无量纲常数 a，即精细结构常数。问题是量子风水学，常数 a 将这三个理论联系在一起有什么深奥的奥秘吗？另外，常数a的值约为1/137，这是什么意思？这个谜一样的值多年来一直困扰着物理学家，以至于关于它，物理学家费曼有一段非常有趣的文字：

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：