简单的稳定婚姻匹配( 二 ) _匹配

D=[a;B1];%%这里输出的是1到n编号女士对应的配偶的编号
End
输入说明：这里的A ， B存储的是编号，而不是第一喜欢的人
Matlab的文件输入输出问题：
四、案例的测试
用书上那个例子：见算法设计与分析基础293页
性别
编号
1
2
3
男士
Bob
Jim
Tom
女士
Ann
Lea

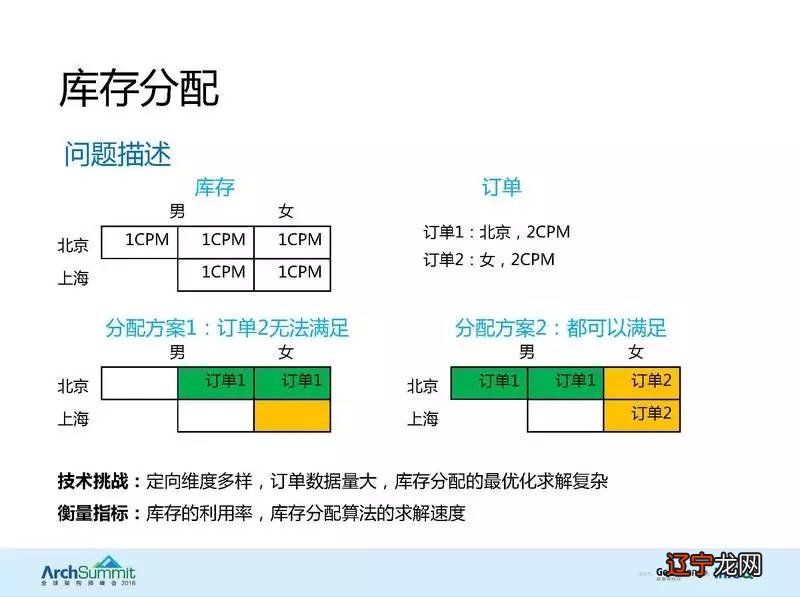
Sue
那么男士的优先级顺序为：女士的优先级顺序为：
A= [2,1,3B= [2,3,1
2,3,13,1,2
3,2,1]2,3,1]
A的每一行分别是Bob,Jim和Tom心中对理想对象的优先级顺序
同理， B的每一行分别是Ann,Lea和Sue心中对理想对象的优先级顺序。
>>Match(A,B)
ans=
123
132
可以从结果分析，女士Ann和Bob结婚，女士Lea和Tom结婚，女士Sue和Jim结婚
和书上的结果是一样的。
五、算法的局限性
1.输出的局限性：该算法显然会输出一个稳定的匹配，在这个匹配中，所有的男生和他们的第一选择相配，但是对女生并不如此。例如上面的从B中知道Ann最喜欢的是2号男生Jim ，第三喜欢才是BOb,然后Bob第二喜欢的是Ann, ，男生可以不断去表白，选择自己比较喜欢的男生，女生就只能比较男友和更换男友，这样，女生可能等不到最喜欢的男友的表白，游戏就结束了。
如果想要女生占优势，那么需要把女士和男生的输入顺序对换过来。
2.时间的效率性改进：为了快速求出所有的稳定匹配结果,提出了基于先序遍历森林的快速枚举算法。由Gale-Shapley算法的性质得到一个定理及其推论,利用得到的推论对算法做了进一步改进和优化。在满足推论的特定条件下,提高了算法的执行效率
六、具体的应用
应用于测试资源匹配的婚姻稳定算法改进
下一代自动测试系统中将实现测试资源的动态分配,我们使用婚姻稳定(StableMarriage)算法来解决测试过程中测试资源与被测设备的匹配问题,使用择偶倾向队列缩减模型对求解典型"婚姻稳定"问题的Gale-Shapley(G-S)算法进行优化.该模型中使用择偶倾向队列描述婚姻稳定问题中匹配优先顺序,该队列会随着算法进行逐渐缩短,在简化数据规模的同时优化了处理婚姻稳定问题的G-S算法处理流程,改进后算法实现无效匹配请求的预先清除,从而使用后来请求优先的原则对匹配请求进行处理机制,对原有算法的时间空间成本实现了优化,适应了测试资源匹配任务的需求.
参考文献：孙昱付少波张天培李长安《应用于测试匹配婚姻算法的优化改进》

以上关于本文的内容，仅作参考！温馨提示：如遇专业性较强的问题（如：疾病、健康、理财等），还请咨询专业人士给予相关指导!

「辽宁龙网」www.liaoninglong.com小编还为您精选了以下内容，希望对您有所帮助：